Een grafiek is een manier om een verband (samenhang) te ontdekken tussen twee grootheden.

In de natuurkunde doen je aan onderzoek. Tijdens zo'n onderzoek (experiment) doe je meestal metingen aan twee grootheden. De meetresultaten zet je in een tabel.

Uit die tabel wordt lang niet altijd duidelijk of de twee gemeten grootheden met elkaar samenhangen. Door van die metingen een grafiek te tekenen, wordt meteen duidelijk OF er een samenhang is tussen die grootheden en wat die samenhang dan is.

Voorbeeld-1:

Don de Jong en Gio Latooy gaan water aan de kook brengen. De twee gemeten grootheden bij deze proef zijn Temperatuur en Tijd. Elke 15 seconden roept Don: "YEP!!"" en op dat moment meet Gio de temperatuur van het water. De resultaten van die metingen staan in onderstaande tabel.

T (°C)	t (s)
15	0
22	15
29	30
35	45
42	60
47	75
53	90
59	105
66	120
73	135
81	150
88	165
94	180
100	195

De vraag is of de twee grootheden met elkaar samenhangen. Je zegt dan dat je een verband zoekt tussen deze twee grootheden. Uit de tabel blijkt dit niet direct. (Als je het wèl meteen ziet, ben je al hard op weg een briljant wetenschapper te worden...).

Daarom ga je deze gegevens uitzetten in een grafiek. Bij het tekenen van een grafiek gelden bij natuurkunde de volgende regels:

Regels bij het maken van een grafiek:

1. RUITJESPAPIER

Werk op ruitjespapier. Hoe groot de ruitjes zijn, is niet zo belangrijk.

2. POTLOOD

Gebruik voor ALLES in en om de grafiek een POTLOOD. Ook de getallen en de symbolen bij de assen moeten met potlood.

3. ASSEN

Maak beide assen in het begin 10 cm lang. Als later blijkt dat daardoor een meting er net niet op past, mag je de as best een ietsje verlengen.

4. GROOTHEDEN EN EENHEDEN

Bij elke as zet je:

* Het symbool van de gemeten grootheid.

* Het symbool van de bijbehorende eenheid erachter en tussen haakjes.

* Een pijl die laat zien in welke richting de grootheid toeneemt.

(Als er tijd gemeten is zoals nu, zet deze dan altijd horizontaal)

5. GETALLEN LANGS ASSEN

Kijk naar de hoogst gemeten waarde van de grootheid in de tabel. Kies een 'mooi getal' in de buurt van die hoogste waarde. Zet dat mooie getal zo ver mogelijk langs de as uit, maar wel zodanig dat je de as in gelijke stukjes kunt verdelen!

Die 'gelijke stukjes'moeten wel een beetje mooi gekozen zijn.

Mooi gekozen is bijvoorbeeld:

- 10, 20, 30, 40, enz.

- 20, 40, 60, 80 enz.

- 25, 50, 75, 100

NIET mooi gekozen is bijvoorbeeld:

- 7, 14, 21, 28, 35, enz.

- 3, 6, 9, 12, enz.

6. MEETPUNTEN UITZETTEN

Zet de meetwaarden uit in de grafiek met een rondje met een stip erin OF met een kruisje.

Gebruik NIET een gewoon puntje: als je de grafiek tekent, zie je de puntjes niet meer en dan kan de docent niet meer controleren of je je meetwaarden goed in de grafiek hebt uitgezet. Dat kost je punten, zonde!!

7. LIJN TEKENEN

Kijk of de punten op een rechte lijn liggen. Als ze dat ongeveer liggen, teken dan een rechte( = gebruik je geo!) ) lijn die zo goed mogelijk door al die punten gaat. Dit noemen we een 'beste rechte'. Het verband tussen deze twee grootheden heet dan een lineair verband. Als die rechte lijn dan ook nog eens door de oorsprong zou gaan, zou het verband een 'recht evenredig' verband heten. Een recht-evenredig verband is dus ook een lineair verband.

Als de punten bij lange na niet op een rechte lijn liggen kun je misschien een vloeiende kromme door je meetpunten heen tekenen. Zie verderop. Dat heet dan een exponentieel verband.

Ga zeker NIET punt met punt verbinden.

Hoe ziet de grafiek van Don en Gio er dan uit:

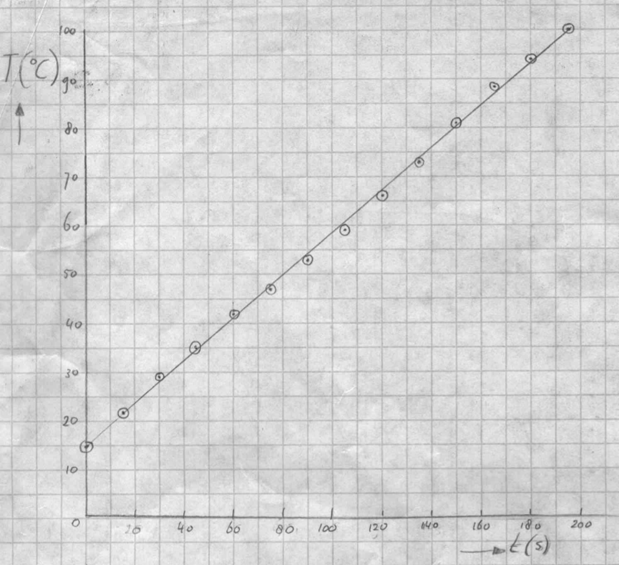
Controleer in de grafiek of aan alle regels is voldaan.

Bekijk hoe de schaalverdeling is gekozen. Controleer dat de toename langs de assen steeds gelijk is. Bijvoorbeeld: 20, 40, 60, 80, 100, enz. voor de tijd. Wat NIET mag is: 20, 45, 60, 70, 85 enz.

Zie dat niet alle punten precies op 1 rechte lijn liggen? Dit komt door foutjes tijdens de proef (meetfoutjes, afleesfoutjes, instrumentele foutjes). Maar wèl duidelijk is dat door deze meetwaarden een rechte lijn kan worden getrokken. die trek je dan zo goed mogelijk door alle punten en noem je een 'beste rechte'. Het verband tussen temperatuur en tijd is bij deze proef dan ook LINEAIR. Dat wil zeggen, dat bijvoorbeeld elke 20 seconden de temperatuur met een vast bedrag toeneemt (en dat de grafiek niet door de oorsprong gaat).

Voorbeeld-2:

Royalistiq en Milan Knol gaan de weerstand (R) van een metalen draad meten bij verschillende temperaturen. De resultaten staan in onderstaande tabel:

R (Ω)	T (°C)
10,0	20
10,6	25
11,6	30
13,0	35
15,0	40
17,3	45
20,0	50
23,5	55
29,5	60
37,5	65
47,5	70

Of je nu weet wat 'weerstand' is of niet, is nu niet belangrijk. Het gaat erom hoe je de getallen in de grafiek zet m.b.v. de regels.

Controleer de grafiek met hulp van de regels. Zie je dat het verband hier NIET lineair is? Door de punten kun je wel een vloeiende kromme tekenen.

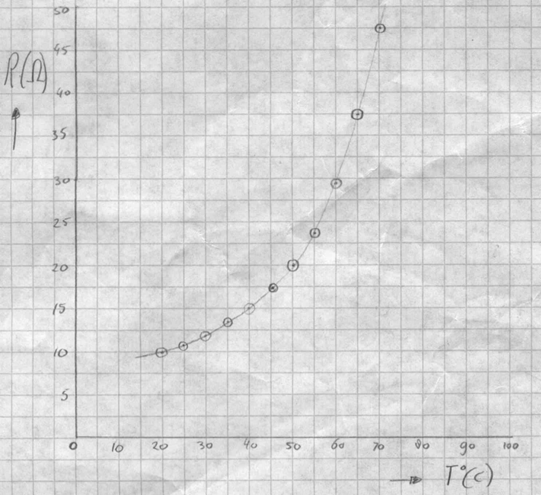
Voorbeeld-3:

Max Verstappen en zijn vader Jos gaan racen in een Porsche 911 Turbo S. Max geeft vanuit stilstand flink gas en Jos kijkt elke 2 seconden hoe hard ze rijden. De resultaten staan in de tabel:

v (km/h)	t(s)
0	0
50	2
100	4
150	6
200	8
250	10
280	12
315	14
315	16
315	18
315	20

En hier de grafiek:

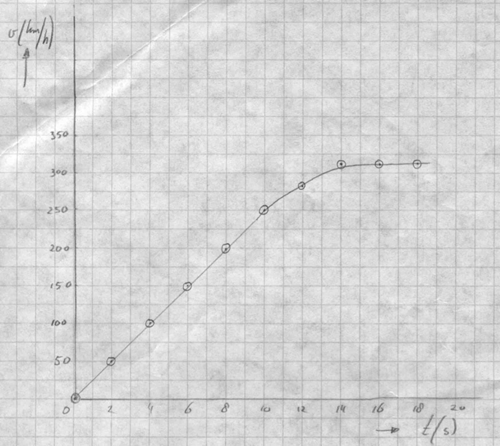
Controleer de grafiek met hulp van de regels. Zie je dat het verband in het begin recht-evenredig is (dit kun je al in de tabel zien) maar dat dit op het einde niet het geval meer is. De grafiek is dus in het begin een rechte lijn en wordt later 'afgevlakt'. Waar dat precies gebeurt is niet bekend. Je moet dat dus een beetje inschatten.

Dylan Haegens en Marit Brugman meten de snelheid van een optrekkende auto. De resultaten staan in onderstaande tabel:

v(km/h)	t(s)
0	0
10	1
20	2
30	3
40	4
50	5
60	6

Teken de grafiek. Gebruik de regels.

Nienke Plas & Défano Holwijn meten de afstand (s) die een breedbek kikker aflegt in een bepaalde tijd. De resultaten staan in onderstaande tabel:

s(m)	t(s)
0	0
1,28	1
2,56	2
3,92	3
5,19	4
6,52	5
7,81	6
9,14	7
10,42	8

Teken de grafiek. Gebruik de regels.

Sjek en Vloetje meten de afgelegde afstand (s) van een roofvogel per seconde tijdens een duikvlucht. (Hoe doen ze dat toch?? Wat een helden!). De resultaten staan in onderstaande tabel:

s(m)	t(s)
0	0
6	1,0
10	1,5
15	2,0
22	2,5
30	3,0
40	3,5
56	4,0
72	4,5
90	5,0
108	5,5

Teken de grafiek.

Laat de docent al je grafieken controleren. Hij/zij controleert ze alleen als je alle voorbeelden hebt uitgewerkt en als in één oogopslag blijkt dat je netjes hebt gewerkt.

Zoals al gezegd zoek je naar verbanden tussen grootheden. Er zijn een aantal veel voorkomende verbanden, te weten:

Lineair verband

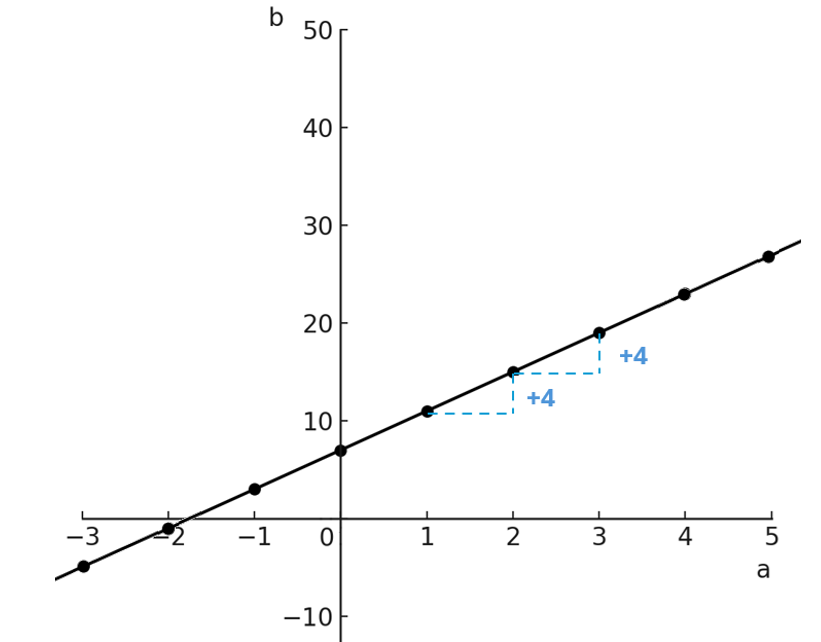
Grafiek: rechte lijn, niet door de Oorsprong

Uitleg: de verandering is constant (steeds hetzelfde)
In de grafiek zie je b steeds met 4 toenemen als a met 1 toeneemt. De toename is dus steeds gelijk en ken je in de wiskunde als het hellingsgetal.

Recht-evenredig verband

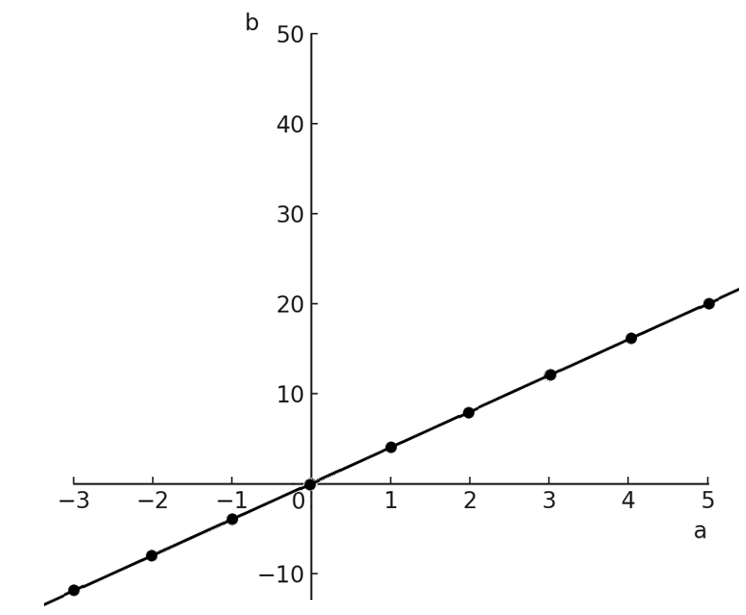
Grafiek: rechte lijn door de Oorsprong.

Uitleg: Als de ene grootheid x keer zo groot wordt, wordt de andere grootheid ook x keer zo groot.

Omgekeerd evenredig verband

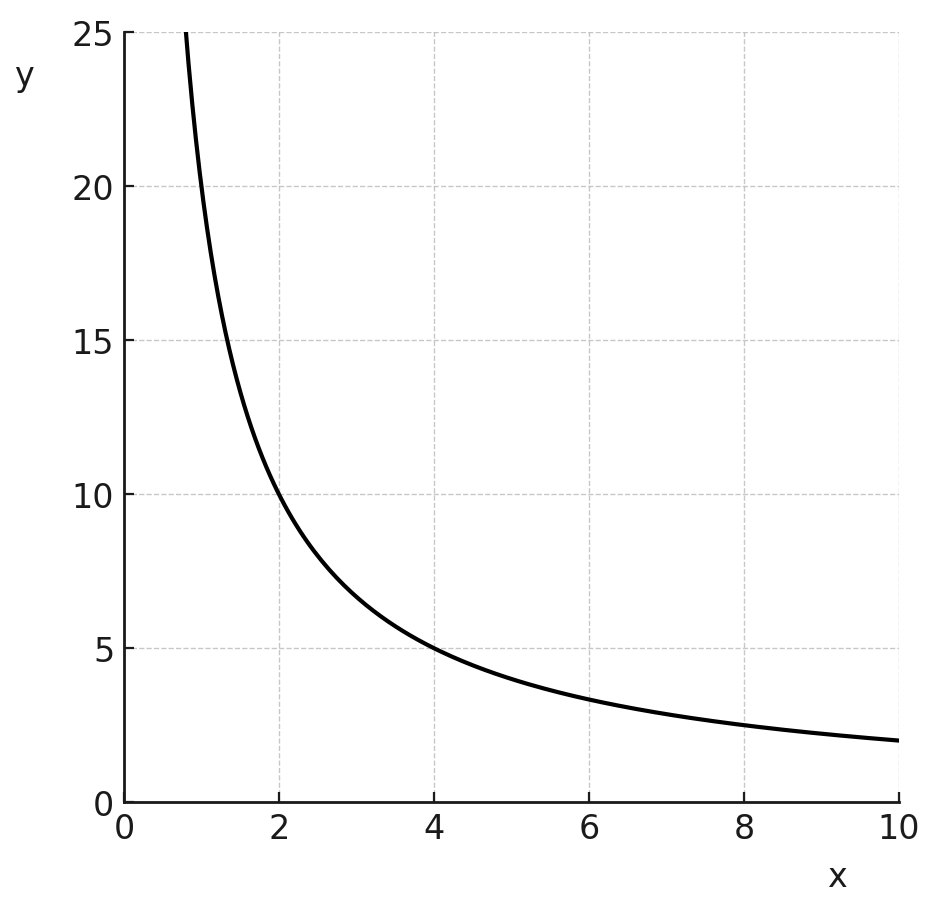
Grafiek: vloeiende kromme.

Uitleg: Als de ene grootheid x keer zo groot wordt, wordt de andere grootheid x keer zo klein. Deze vloeiende kromme noem je een hyperbool: de grafiek nadert de assen maar zal deze nooit raken.

Exponentieel verband

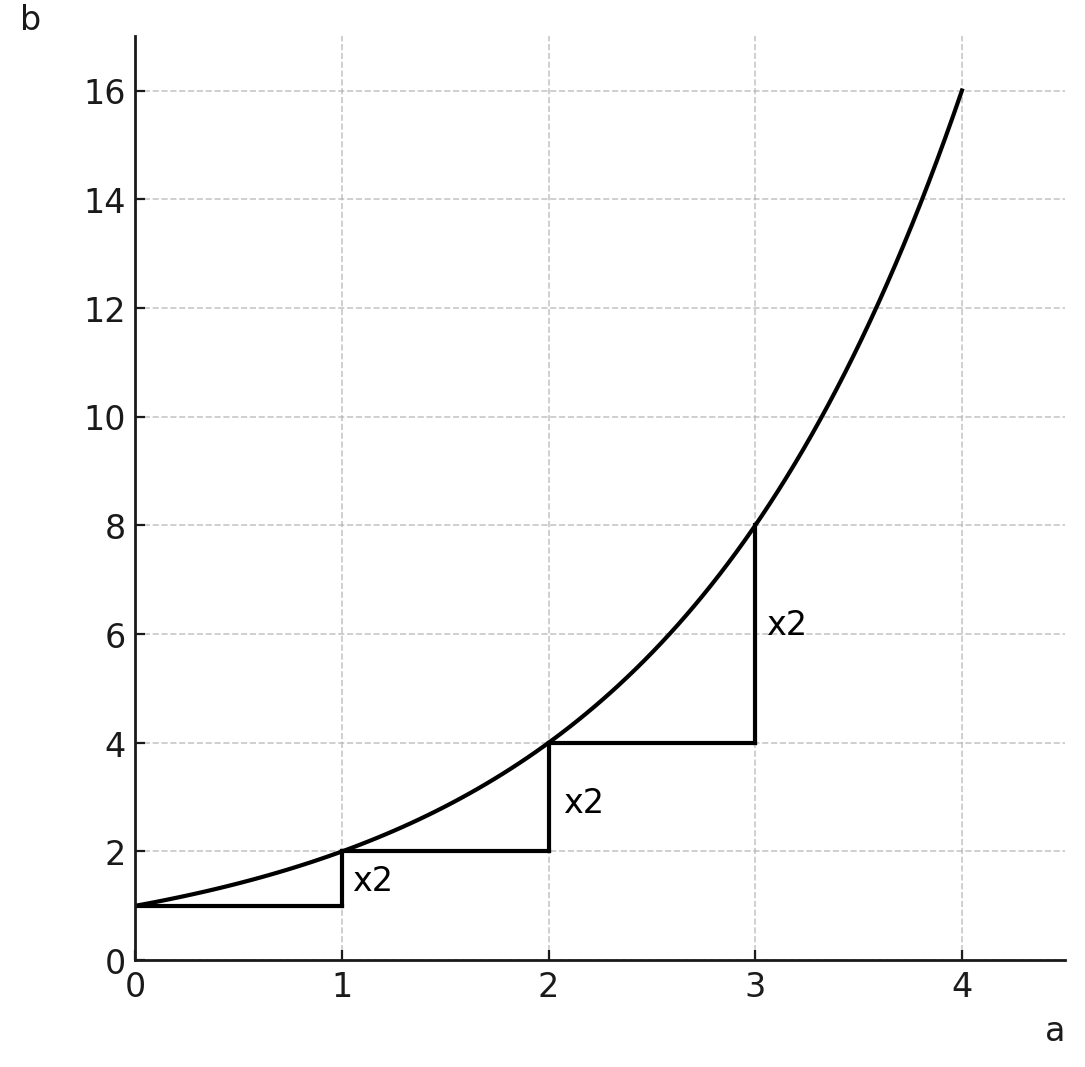
Grafiek: vloeiende kromme.

Uitleg: De grootheid b wordt elke keer vermenigvuldigd met dezelfde getal. Dit getal noemen we de groeifactor. In deze grafiek is de groeifactor 2